Creating the longest possible Ski Jump in The Games: Winter Challenge
After spending way too much time getting side-tracked with investigating the copy protection measures, it is time to return to the actual reason I started looking into The Games: Winter Challenge to begin with: The quest to create the optimal ski jump and see how far you can push the game.
One of my initial questions was already answered, namely whether it’s possible to jump farther than 100 meters, a feat that I never managed as a kid. One of the hidden copy protection measures of the game limits how far you can jump when they are active, and without them I jumped farther without too much trouble:
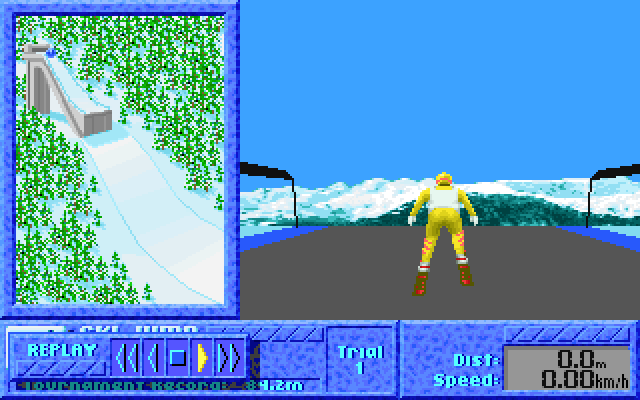
I’d like to think that I’m just better at video games than I was as a kid, but realistically I likely could have achieved this decades ago without the artificial limitations the copy protection adds.
But the big question of “how far can you go?” still remained. I see two possible avenues for going about answering it. One is to build some form of harness to allow individually controlling the inputs the game receives, advancing one frame at a time and using savestates to try many different input sequences to see which produces the best result. This is how most tool-assisted speedruns for video games are created, using special emulators which have those functions built-in. However, this method has some drawbacks. For one, it is limited by your understanding of and creativity within the game: if there is some hidden mechanic you don’t know about, you won’t be able to exploit it. Also, if there are too many different possibilities to try, it can be very tedious to try them by hand, and doing it programmatically can be fairly slow because you need to emulate the whole game millions of times.
Instead, I will be going for a more analytical approach. We will not be playing the game at all, and instead crack the game binary open and deeply understand how it functions. By learning all the details of how the game runs the simulation, we can analyze how it represents the game state, how it runs its physics simulation, and how it determines the actual distance traveled. Maybe by this we will learn that the answer is as simple as “keep as straight as possible to maximize distance”. Likely the logic will be much more complicated than that though, and it should be possible to create a model re-implementation of the ski jump logic, extracting only the relevant parts and run much more efficient simulations on it. Then, by learning how the game’s replay file format works, we can create our own synthetic replays using the input sequences we found from our simulations, and play them back in the game, achieving the optimal ski jump entirely outside the game itself.
The basic mechanics of the ski jump event
To start off, let’s go over how a ski jump in the game works in general. There are four main phases for each jump: First, you go down the jumping ramp and can move the jumper left and right, counteracting random winds pushing you around. Then, you jump off the take-off table, by pressing down at the right time, which determines how high your jumper will lift off. Next, you fly over the hill, and can press up and down in order to adjust the angle of the skis for a more aerodynamic position, again with some wind randomly pushing against you. Finally, you press Enter as you approach the ground to land safely.
The game itself, as well as its manual, give some hints as to how you’re supposed to use your controls in order to jump farther. While going down the ramp, if you stray too far left or right, the game renders puffs of snow and plays a corresponding sound, indicating to you that you’re going off the track and are slowing down. During the flight section, while the game itself doesn’t give you any direct feedback on whether what you’re doing is good, the game’s manual recommends keeping the skis parallel during the flight to minimize drag. This “parallel style” is a great reminder of the game’s age, as it was in fact the dominant ski jump technique up until the early 90’s when this game was created, and was since replaced by the now dominant “V-style” of forming a V-shape with the skis. The game does allow you to form a V-shape as well, but it’s unlikely that it simulates air resistance in any meaningful way, and I assume that what is optimal is what the developers wanted you to do, instead of what is actually better in the real world.
Overall, this surface-level analysis goes by what the game itself tells us is good or bad, but there is no guarantee that this is actually true. For one, there could be hidden mechanics that influence the jump which are not explained directly. And even if that isn’t the case, what the developers intended to be the optimal strategy, and what the optimal strategy actually is, can be very different things. It’s quite plausible that there are some emergent behaviors that the developers didn’t anticipate, but which can help us achieve better results. There are numerous well-known examples in video games where this happens, like the famous Backwards Long Jump in Super Mario 64, which is an unintended consequence of Mario’s movement system which allows to reach higher speeds than the developers expected were possible.
Decoding the replay file format
In order to find out whether such hidden or emergent mechanics do exist, I need to actually crack the game open and look inside. All the setup work I did in part 1 is now paying off, allowing the game to load into the disassembler nicely and in one piece.
However, I don’t have a lot of good leads yet as to where in the binary to look. So to start out I decided to look into the replay file system first. This is because the file I/O needed to read the replay can be easily identified in DOSBox’s emulator, providing a starting point, and the files can be externally manipulated to verify what impact each part has.
First, let’s take a look at what a replay file looks like on the inside, using the attempt shown above as an example:
4E 02 F8 00 0E 00 AC 01 BA 01 94 00 25 00 00 00
03 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 05 00 00 00 00 00 1B 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
7D 1E 51 36 00 00 00 00 00 00 3F 00 00 00 40 FF
FF FF 00 00 00 00 FF FF FF FF C0 01 00 00 00 00
00 08 00 00 00 00 00 00 00 00 0E 00 02 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 FF FF FF FF C0 01 00 00
00 00 F7 23 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
01 00 00 00 00 00 00 00 00 00 FD 7F 00 00 00 00
FD 7F 00 00 01 00 00 00 03 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 01 00 00 00 00 00 00 00
01 00 00 08 00 7E 00 00 00 00 00 00 FF FF FF FF
C0 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00
20 00 80 02 00 01 00 00 00 00 1B 00 3F 0C 03 00
41 40 1B 00 1C 40 1E 00 C2 40 1B 00 02 40 1E 00
C2 40 1B 00 01 40 1E 00 C4 40 1B 00 0B 40 1E 00
C4 40 1B 00 0D 40 1B 00 3F 0C 1E 00 C3 40 1B 00
04 40 1E 00 C1 40 1B 00 06 40 1E 00 C2 40 1B 00
06 40 33 00 50 41 1B 00 02 40 03 00 41 40 1B 00
07 40 03 00 42 40 1B 00 10 40 1B 00 3F 0C 03 00
42 40 1B 00 0A 40 33 00 42 41 1B 00 09 40 33 00
42 41 1B 00 02 40 1B 00 01 54 1B 00 01 44 1B 00
04 40 1E 00 DB 40 1B 00 3B 0C 1B 00 36 40
There is not a lot of data in these files, and from some educated guessing and checking different replays, we can already guess the structure.
The first 14 bytes are some header structure, with the initial two bytes always equal the total size of the replay data (using Little-endian byte order), and the remaining bytes representing some lengths and offsets within the file. From this we can learn that there are two blocks of data in the file.
The first section is basically identical across all replay files, apart from a few bytes which appear to change randomly: one byte at offset 0x10, 4 bytes at offset 0x50 and 2 more bytes at offset 0x102.
Modifying these values and observing the effects in game lets us see what they do: The value at 0x10 changes the color of the suit the jumper is wearing, which is randomly assigned by the game for each attempt. The values 0 to 15 represent the different valid color combinations a jumper can have, and going beyond it will cause glitched color palettes to be used, presumably read from beyond the table which holds the palette data.
Modifying the values at 0x50 alters the trajectory the jumper takes, so presumably those are the RNG seed the game uses for the wind deflections. Modifying the values at 0x102 has a similar result, but only affects the position of the skis while airborne, and appears to encode the initial angle the skis are in when lifting off.
The second block of data varies in length and content between files, and appears to encode the inputs recorded during the attempt. It is always a multiple of 4 bytes long, and there’s a noticeable repeating pattern every 4 bytes in the data, suggesting that each block of 4 bytes encodes an input in some way.
This lets us build some mental model of how the replay system works: A replay consists of two parts, a savestate which determines the initial game state, and a sequence of inputs which then tells the game how to behave over time. The game runs the simulation just like when playing the game, but instead of using the player’s inputs it takes the pre-recorded inputs from the file to reproduce the previous attempt. The initial state is mostly identical between replay files because the initial state of a ski jump is always the same. For longer disciplines like Biathlon, replays don’t always record the full attempt and can start somewhere in the middle, which is where this initial savestate would matter much more.
So the example replay file contents break down like this:
# Header information
4E 02 # file size in bytes
F8 00 # number of frames in the replay
0E 00 # offset of the savestate data in bytes
AC 01 # size of the savestate data in bytes
BA 01 # offset of the input data in bytes
94 00 # size of the input data in bytes
25 00 # number of 4-byte input blocks
# Savestate data, mostly identical across replays
00 00 03 00 00 00 00 00 00 00 00 00 00 00 00 00 # 03 = yellow suit
00 00 00 00 00 00 00 00 05 00 00 00 00 00 1B 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 7D 1E 51 36 00 00 00 00 00 00 3F 00 00 00 # 7D 1E 51 36 = RNG seed
40 FF FF FF 00 00 00 00 FF FF FF FF C0 01 00 00
00 00 00 08 00 00 00 00 00 00 00 00 0E 00 02 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 FF FF FF FF C0 01
00 00 00 00 F7 23 00 00 00 00 00 00 00 00 00 00 # 0x23F7 = initial ski angle
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 01 00 00 00 00 00 00 00 00 00 FD 7F 00 00
00 00 FD 7F 00 00 01 00 00 00 03 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 01 00 00 00 00 00
00 00 01 00 00 08 00 7E 00 00 00 00 00 00 FF FF
FF FF C0 01 00 00 00 00 00 00 00 00 00 00 00 00
00 00 20 00 80 02 00 01 00 00 00 00
# Input data, blocks of 4 bytes
1B 00 3F 0C 03 00 41 40 1B 00 1C 40 1E 00 C2 40
1B 00 02 40 1E 00 C2 40 1B 00 01 40 1E 00 C4 40
1B 00 0B 40 1E 00 C4 40 1B 00 0D 40 1B 00 3F 0C
1E 00 C3 40 1B 00 04 40 1E 00 C1 40 1B 00 06 40
1E 00 C2 40 1B 00 06 40 33 00 50 41 1B 00 02 40
03 00 41 40 1B 00 07 40 03 00 42 40 1B 00 10 40
1B 00 3F 0C 03 00 42 40 1B 00 0A 40 33 00 42 41
1B 00 09 40 33 00 42 41 1B 00 02 40 1B 00 01 54
1B 00 01 44 1B 00 04 40 1E 00 DB 40 1B 00 3B 0C
1B 00 36 40
I tried to determine the structure of the input blocks using the same method by cross-checking different input files, but some blocks didn’t seem explainable with this method, so I proceeded to continue from the other end, by looking into the game’s code which reads the file.
Starting at where the file is being opened, the game allocates blocks of memory for each of the different sections, and copies the data into memory. The savestate data is handled in multiple chunks which are loaded from and into different places in memory, effectively allowing to save and load a savestate. Where those memory regions are differs by discipline, and for the Ski Jump there are 4 chunks which make up the savestate:
[0x7a3c - 0x7a7e](0x42 bytes) - Contains the player data, like the color of the suit (can also contain more data like the chosen name and flag in tournament mode)[0x69f6 - 0x69fa](4 bytes) - Contains the RNG seed[0x43f8 - 0x4504](0x10c byte) - Presumably contains ski jump state data, including the initial ski angle[0x4504 - 0x455e](0x5a byte) - Presumably contains also ski jump state data
This gives us a direct mapping from the data we see in the replay file to the memory addresses we see in the game’s code. It also gives us hints when reading the game’s code as to which variables will be associated with the ski jump event: If they are part of the save state, they are apparently important. Notably the last two memory segments are contiguous, and are split up because they presumably, in the developer’s mind, hold different types of data about the game state, but we don’t know which yet.
Reading further through the code, we find the place where the input data from the replay file is being used:
seg017:3638 load_replay_inputs:
seg017:3638 mov di, ax
seg017:363A shl di, 1
seg017:363C shl di, 1
seg017:363E add di, offset input_data_buffer ; seek to current input block
seg017:3642 test byte ptr [di+2], 3Fh ; check length
seg017:3646 jnz short process_input_block ; if zero, read next input block, otherwise continue using current block
seg017:3648 mov ax, parse_replay_header_e_52F52
seg017:364B shl ax, 1
seg017:364D shl ax, 1
seg017:364F add ax, parse_replay_header_4_alloc_offset_52F48
seg017:3653 mov dx, parse_replay_header_6_alloc_segment_52F4A
seg017:3657 mov bx, ax
seg017:3659 mov es, dx
seg017:365B inc parse_replay_header_e_52F52
seg017:365F mov ax, es:[bx]
seg017:3662 mov dx, es:[bx+2] ; reads next four bytes from the replay file into buffer
seg017:3666 mov [di], ax
seg017:3668 mov [di+2], dx
seg017:366B process_input_block:
seg017:366B mov ax, [di]
seg017:366D mov [bp+direction_input], ax
seg017:3670 dec word ptr [di+2] ; reduce length by one
seg017:3673 mov si, [di+2]
seg017:3676 and al, 7
seg017:3678 sub al, 3
seg017:367A mov replay_input_x_direction, al ; ranges from [-3,3]
seg017:367D mov cl, 3
seg017:367F mov ax, [bp+direction_input]
seg017:3682 shr ax, cl
seg017:3684 and al, 7
seg017:3686 sub al, cl
seg017:3688 mov replay_input_y_direction, al ; ranges from [-3,3]
seg017:368B mov cx, offset replay_input_direction_magnitude
seg017:368E push cx
seg017:368F mov cx, offset replay_input_angle ; values 0-ff, 0=right, counter-clockwise
seg017:3692 push cx
seg017:3693 mov cx, offset replay_input_direction ; values 0-8, 0=center, 1=up, clockwise
seg017:3696 push cx
seg017:3697 push ax
seg017:3698 mov al, replay_input_x_direction
seg017:369B push ax
seg017:369C call calculate_input_magnitude_direction_angle ; calculates derived values, not used in Ski Jump
seg017:36A1 add sp, 0Ah
seg017:36A4 mov cl, 6
seg017:36A6 mov ax, si
seg017:36A8 shr ax, cl
seg017:36AA and al, 0Fh
seg017:36AC mov replay_input_bits_6_to_10, al
seg017:36AF mov ax, si
seg017:36B1 and ax, 400h
seg017:36B4 cmp ax, 1
seg017:36B7 sbb al, al
seg017:36B9 inc al
seg017:36BB mov replay_input_bit_10, al
seg017:36BE mov ax, si
seg017:36C0 and ax, 800h
seg017:36C3 cmp ax, 1
seg017:36C6 sbb al, al
seg017:36C8 inc al
seg017:36CA mov replay_input_bit_11, al
seg017:36CD mov ax, si
seg017:36CF and ax, 1000h
seg017:36D2 cmp ax, 1
seg017:36D5 sbb al, al
seg017:36D7 inc al
seg017:36D9 mov replay_input_bit_12, al
seg017:36DC mov ax, si
seg017:36DE and ax, 2000h
seg017:36E1 cmp ax, 1
seg017:36E4 sbb al, al
seg017:36E6 inc al
seg017:36E8 mov replay_input_bit_13, al
seg017:36EB mov ax, si
seg017:36ED and ax, 4000h
seg017:36F0 cmp ax, 1
seg017:36F3 sbb al, al
seg017:36F5 inc al
seg017:36F7 mov replay_input_bit_14, al
seg017:36FA mov ax, si
seg017:36FC and ax, 8000h
seg017:36FF cmp ax, 1
seg017:3702 sbb al, al
seg017:3704 inc al
seg017:3706 mov replay_input_bit_15, al
seg017:3709 pop si
seg017:370A pop di
seg017:370B mov sp, bp
seg017:370D pop bp
seg017:370E retf
This code helps us decipher how each input block is constructed: Each block represents a run-length encoded sequence of frames where the same input is being held, and is made up of two 2-byte words. The first word encodes the directional inputs, with the lowest three bits being the x input, and the next three bits being the y input. Each direction can have values from 0 to 6, representing directional amplitudes from -3 to 3. The second word contains how many frames the inputs were held, and a set of additional bits corresponding to individual keys that can be pressed, like the Enter key for landing a jump.
So an example input block 33 00 42 41 would be decoded like:
0x0033 0x4142
0000000000 110 011 0 1 0 0 0 0 0101 000010
y=3 x=0 | len = 2
-> holding down no Enter for two frames
Many of the additional input bits turn out to be completely unused in the Ski Jump event, only one of them, bit 12 representing the Enter key, is accessed at all, so we don’t need to worry too much about what all the others represent.
Input format weirdness and joystick support
However, this still doesn’t fully explain the input blocks we’re seeing in the input files, there appear to be additional blocks that shouldn’t be part of the inputs at all, and adding up all the lengths of the blocks, we find the total to be exactly twice as large as we’d expect.
This mystery can be resolved when looking at the code which then processes the inputs in the ski jump event:
seg005:1C94 ski_jump_read_inputs proc near
seg005:1C94 sub ax, ax
seg005:1C96 call save_load_replay_inputs ; read inputs with ax = 0
seg005:1C9B mov al, replay_input_x_direction
seg005:1C9E cbw
seg005:1C9F mov ski_jump_left_right_input, ax ; transfer left/right input
seg005:1CA2 mov al, replay_input_y_direction
seg005:1CA5 cbw
seg005:1CA6 mov ski_jump_up_down_input, ax ; transfer up/down input
seg005:1CA9 mov al, replay_input_bit_12
seg005:1CAC sub ah, ah
seg005:1CAE mov ski_jump_enter_pressed, ax ; transfer enter press
seg005:1CB1 cmp al, ah
seg005:1CB3 jz short check_input_again
seg005:1CB5 call reset_enter_key ; makes it so that enter is only registered for one frame
seg005:1CBA check_input_again:
seg005:1CBA mov ax, 2
seg005:1CBD call save_load_replay_inputs ; read inputs again, with ax = 2
seg005:1CC2 cmp replay_input_x_direction, 0 ; if any relevant inputs are present, override input with this one
seg005:1CC7 jnz short override_input
seg005:1CC9 cmp replay_input_y_direction, 0
seg005:1CCE jnz short override_input
seg005:1CD0 cmp replay_input_bit_12, 0
seg005:1CD5 jz short return
seg005:1CD7 override_input:
seg005:1CD7 mov al, replay_input_x_direction
seg005:1CDA cbw
seg005:1CDB mov ski_jump_left_right_input, ax ; transfer left/right input
seg005:1CDE mov al, replay_input_y_direction
seg005:1CE1 cbw
seg005:1CE2 mov ski_jump_up_down_input, ax ; transfer up/down input
seg005:1CE5 mov al, replay_input_bit_12
seg005:1CE8 sub ah, ah
seg005:1CEA mov ski_jump_enter_pressed, ax ; transfer enter press
seg005:1CED cmp al, ah
seg005:1CEF jz short return
seg005:1CF1 call reset_enter_key
seg005:1CF6 return:
seg005:1CF6 retn
The input reading happens twice each frame! This is because there are two possible sources for inputs, the keyboard and a joystick. The game has joystick support, and allows you to play any discipline with it, so on each frame there may be inputs coming from either device.
This also explains why the x and y directional inputs can have 7 different values from -3 to 3: The keyboard input will only ever produce values of -3, 0, or 3, but the joystick as an analog device can produce any value in the range.
The way the game handles the different input sources means that at any time there are two input blocks which are active at the same time, one for each device, and the second input, the keyboard, overrides any joystick inputs when used. This has some weird consequences for the structure of the inputs in the replay files: The input blocks for both devices are interleaved in the same list, but because the blocks can have different lengths, it’s not as simple as them alternating. Instead, each next block belongs to whichever device runs out of inputs in its current block first. So in practice, given players typically only use one input device at a time, this means that the majority of the blocks belong to the used input device, with only sporadically interleaved empty blocks for the second device every 63 frames, which is the maximum length an input block can have.
With this knowledge, we can now completely decode how the replay files store the inputs, extract them from existing replays, and even create our own input sequences. Additionally, we found out where the variables responsible for the game state are located, and where the inputs are read and processed. This should give us enough starting points to reverse-engineer the game logic for the ski jump event itself.
Disassembling the game logic
Since I already knew where the inputs are being processed, it was easy to discover where it is called to find the main business logic of the ski jumping event, which is executed once every frame to move the game state forward. Actually understanding what it does is not nearly as easy though, and I still have no indications how the game state is actually represented and what any of the memory values might mean, so I just need to start somewhere, try to understand what some part of the code does, guess what different places in memory might represent, and build up the rest from there.
The one known variable I do have is from the hidden copy protection of the event, which checks whether the jump’s distance is more than 86.7 meters, so I decided to follow that lead and look around the section of code where this value is computed.
In trying to decipher what individual functions do, I found a lot of functions performing very standard operations, like implementing a division of two 32-bit values. The x86 instruction set does have division instructions, but since this is a 16-bit program, the division operations are only for 16-bit values, and a 32-bit division needs to be implemented in software instead. The developers didn’t need to write these functions themselves of course, they were part of the standard library that the Microsoft C Compiler they were using came with, but in DOS there is no dynamic linking and no DLLs to load these functions from, so all standard library functions were embedded into the program itself.
There were some more strange functions though, like this one:
seg016:D472 multiply_shr_15:
seg016:D472 push bp
seg016:D473 mov bp, sp
seg016:D475 mov ax, [bp+arg_0]
seg016:D478 imul [bp+arg_2]
seg016:D47B shl ax, 1
seg016:D47D rcl dx, 1
seg016:D47F mov ax, dx
seg016:D481 pop bp
seg016:D482 retf
This method apparently multiplies two 16-bit values, and then shifts the result right by 15 bits. It seems like a strangely specific operation, but it’s called a lot throughout the code so it must have some special significance.
Looking over some more functions like this one, it eventually dawned on me what is going on:
seg016:25C0 vec3_length:
seg016:25C0 push bp
seg016:25C1 mov bp, sp
seg016:25C3 sub sp, 4
seg016:25C6 push di
seg016:25C7 push si
seg016:25C8 mov si, bx
seg016:25CA push word ptr [si+4]
seg016:25CD push word ptr [si+4]
seg016:25D0 call signed_multiply
seg016:25D5 add sp, 4
seg016:25D8 push word ptr [si+2]
seg016:25DB push word ptr [si+2]
seg016:25DE mov di, ax
seg016:25E0 mov [bp+var_4], di
seg016:25E3 mov [bp+var_2], dx
seg016:25E6 call signed_multiply
seg016:25EB add sp, 4
seg016:25EE push word ptr [si]
seg016:25F0 push word ptr [si]
seg016:25F2 mov si, ax
seg016:25F4 mov di, dx
seg016:25F6 call signed_multiply
seg016:25FB add sp, 4
seg016:25FE add si, ax
seg016:2600 adc di, dx
seg016:2602 add si, [bp+var_4]
seg016:2605 adc di, [bp+var_2]
seg016:2608 push di
seg016:2609 push si
seg016:260A call sqrt
seg016:260F add sp, 4
seg016:2612 pop si
seg016:2613 pop di
seg016:2614 mov sp, bp
seg016:2616 pop bp
seg016:2617 retf
This method appears to calculate the length of a 3-dimensional vector, sqrt(x^2 + y^2 + z^2).
Notably in this function, no shift is performed after the multiplication.
What is going on here is that the game is using 16-bit fixed-point arithmetic.
Sidebar: Fixed-point arithmetic
When representing decimal numbers in a computer, the standard most commonly used today is the IEEE 754 floating point format, which represents numbers in the form
m * 2^ewith a mantissa and an exponent. This format allows representing a wide range of numbers from very small to very big, with a limited amount of precision depending on how large the number is.However,early x86 chips did not have an integrated floating-point unit, and only allowed integer operations. In order to use fractional numbers, programs often used fixed-point numbers instead, as they are much easier to handle in software, at the cost of a smaller range of possible values. In fixed-point numbers, the exponent is a fixed value, and only the mantissa is expressed in the integer. In this case, the fixed-point numbers are using a scaling factor of
2^15-1, which means they can only represent values in the range[-1, 1]through the signed 16-bit integers[-0x7fff, 0x7fff]respectively.
When multiplying two such fixed-point numbers, the arithmetic works out in a way that you need to multiply the respective integers and then scale down the result again by a factor of 2^15 to arrive at the correct value, which explains the pervasive usage of the strange-looking function above. It also explains why other operations like the length calculation above don’t need that scaling factor, because the square root operation effectively cancels the scaling factor out again.
With this in mind, a lot of the other operations I found can be recontextualized as fixed point operations on 3-dimensional vectors of numbers, representing common operations like a dot product, cross product, or vector normalization.
As it turns out, the game actually performs a full 3D physics simulation of the objects in question: The jumper has a position and velocity vector, and forces like gravity and drag are applied to them every frame to update them. The surfaces are actually proper 3D rectangular surfaces, and the game calculates the normal force they are applying to the jumper to counteract gravity and push the jumper along the slope instead of falling through it. It is the text book physics case of an object moving down an inclined plane that is being simulated, and all the forces that are acting on it.
Replicating the simulation
With a basic understanding of how the simulation works and what it’s trying to achieve, I was able to make much more efficient progress on the disassembly. Each method I successfully deciphered I also translated into a function in a higher-level programming language (in this case Rust), which is typically much shorter than the assembly and helps both to keep an overview of the business logic as I understand it so far, and to eventually be a fully-functional replica of the game’s simulation.
This was by far the most time-consuming part of this whole process, but also the most rewarding as it began to click, the pieces were falling into place and I felt I had an actual understanding of how the game works internally.
It also became more clear which parts of the code are important and which aren’t. Many pieces of code perform actions which are necessary in the game, but we can ignore them for the purposes of the simulation we’re trying to create. Examples of this are controlling the position of the camera that renders the scene, introducing random variation in the shown sprites to create animations, creating snow particles to indicate the jumper is slowing down, simulating the skis of the jumper separately when they fall off after crashing, and many more. When I suspected that a function performs an operation that does not contribute to the accuracy of the physics simulation, I skipped over decompiling it.
Ignoring the surrounding scaffolding of the menus to start a new attempts, the actual main loop of the simulation followed a simple cycle:
- The game reads the inputs and stores whether directional inputs or enter were pressed this frame.
- The game updates the player’s animation state based on where they are and which inputs are pressed. This animation state represents the different actions the jumper can perform, like sliding down the ramp, straightening out when lifting off, flying, initiating a landing, and braking on the ground after landing.
- The game applies changes to the simulation based on that animation state, like sliding left or right when going down the ramp, determining how much vertical momentum the jumper gains when lifting off, or adjusting the ski angle when airborne.
- The game performs the actual physics simulation, applying gravity and drag, checking for collisions with the geometry of the ramp and the ground, and updating the player’s position and velocity accordingly.
- The game updates information derived from the physics state, including the velocity displayed on screen and the jump distance, which is the value we aim to maximize.
Ensuring accuracy
After completing the full reconstructed code, the next important step is to make sure it actually matches what the game itself is doing, and fix any mistakes that I may have made in the translation process. Testing this is not that easy, because DOSBox doesn’t provide any convenient way to interact with it in order to compare values programmatically. Of course it is open source, and while I could have modified it to allow for such automation, it is not super relevant to what I’m trying to do, so in this case I chose an easier quick-and-dirty route.
DOSBox allows creating a memory dump at any time, and I know exactly at which memory location the relevant variables for the simulation are stored. So I loaded an example replay, and created a memory dump of the data segment for each frame of the simulation, to serve as golden records for what the value of each variable should be at any point in time, which I can load into my simulation without interacting with DOSBox directly.
Comparing my simulation against this source-of-truth data, I uncovered some minor discrepancies, but those were easy to address and quickly I was able to get it to sync along the whole length of the replay, confirming that my decompilation is accurate to the real game and I didn’t miss anything significant.
Synthesizing a replay
The final important capability we need in order to complete the setup is creating our own replays from the simulation and have them be able to play back in the game. I’ve already reconstructed how the replay file format works earlier when starting the disassembly, so using this knowledge we can manufacture our own replays as well.
For the save state portion, I copy the exact starting state from a real replay file, to ensure the game starts out in a valid initial state. It would be very easy to achieve longer jumps by altering the starting conditions, but this goes against the goal I’m aiming for to create the longest ski jump that is achievable in the game under normal playing conditions. The only two sections I allow myself to modify are the RNG-dependent values which are different for every attempt, the seed of the game’s RNG, and the initial ski angle.
For the input data, even though the game supports two different input sources, there is no benefit to using both since their inputs are combined by the game anyway, so I encode all input into one of the sources, and leave the other one pressing nothing.
To create the inputs for the replay, I wrote a simple brute force search which tries all possible inputs at each step, and attempts to find for the longest jump distance throughout the search space of all possible ski jumps, greedily keeping only the most promising candidates at each step to avoid the combinatorial explosion.
So it was time for the moment of truth, loading the resulting artificial replay in the game:
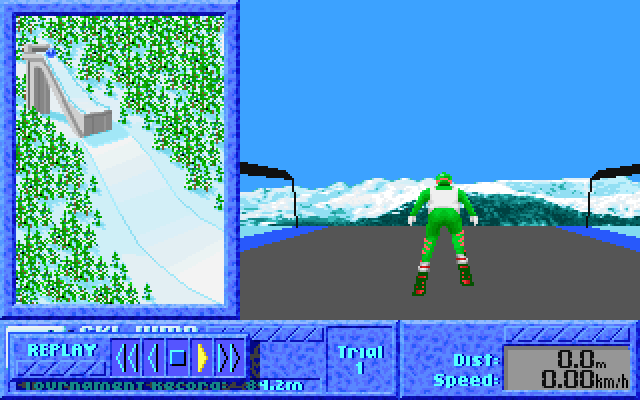
While the jump itself looks underwhelming, this is a huge success. It proves that the whole setup works, that the simulation is accurate beyond the single replay I tested so far, and that the synthetic replays are valid and accepted by the game. All the pieces are in place, the only thing left to do is to use the simulation to optimize the jump and find the farthest possible distance.
Optimizing the search - Simplifying and cutting off bad options
The initial search returned a fairly poor result as seen above, and there are multiple contributing factors which led to this. For one, the search space is actually very big: there are ~80 frames of sliding down the ramp and another ~70 frames of controlling the air movement, where at every frame you have 7 options for directional movement, on top of the timing for lift-off and landing. Secondly, there is the RNG which creates 2^21 different wind patterns, adding to the size of the search space. Lastly, it is hard to predict which actions early in the attempt actually lead to a longer jump distance later, so picking the most promising candidates based on factors like distance traveled or current velocity may easily discard good options early.
One way to reduce the size of the search space is to cut paths which we can be sure will not lead to the best distances, using knowledge about how the simulation works. Since the jumper follows simple projectile motion while airborne, it is obvious that we want to achieve the highest speeds possible to go farther, and that means reducing drag as much as possible. Let’s take a look at the function which calculates the drag:
fn ski_jump_calculate_drag_vec(mem: &mut Mem) {
let mut speed = mem.velocity_magnitude;
let drag_coefficient = match mem.animation_state {
AnimationState::Duck => ((mem.position_vec.x.raw() as i16).abs() >> 4) + 10,
AnimationState::Fly => {
const SKI_JUMP_FLIGHT_ANGLE_BUCKETS: [i16; 8] = [0x600, 0xD00, 0x1300, 0x1A00, 0x2700, 0x2D00, 0x3400, 0x3A00];
const SKI_JUMP_FLIGHT_ANGLE_DRAG_VALUES: [i16; 9] = [14, 12, 8, 6, 4, 6, 8, 12, 14];
SKI_JUMP_FLIGHT_ANGLE_DRAG_VALUES[match SKI_JUMP_FLIGHT_ANGLE_BUCKETS.binary_search(&mem.ski_flight_angle) {
Ok(p) => p,
Err(p) => p,
}]
},
AnimationState::Landing => 40,
AnimationState::Landed => 96,
AnimationState::Crashed => if mem.is_grounded { 280 } else { 8 },
AnimationState::Braking => {
if speed < 40 { speed = 40; }
350
},
_ => 18,
};
mem.drag_vec = mem.normalized_velocity_vec * Fixed16::from_raw_i16(((drag_coefficient as i32 * speed as i32) / -160) as i16);
if mem.ski_jump_upwards_movement_frames != 0 {
mem.drag_vec.y = Fixed16::zero();
}
}
One place additional drag is being applied is when sliding down the ramp: the game chooses a drag coefficient based on where the jumper is on the ramp laterally. If the jumper is in the center (close to position x=0), the least drag is applied, and the farther they are to the sides, the more drag is added. Since there is no apparent upside to going down the side of the ramp, we can cut off any states from our search tree which veer off too far and slow down. This also has the additional benefit that we no longer need to simulate the puffs of snow that appear when going down the side of the ramp, simplifying the simulation itself.
Another instance of unnecessary drag happens in the air: There is a range of optimal ski angles where the drag is minimal, and the further you deviate from that angle, the more drag is being added. More drag just shortens our flight trajectory, so we only need to consider inputs which keep the flight angle in the optimal range.
The final bit of additional drag happens when landing: Once you press enter to initiate the landing, the drag increases dramatically, slowing you down. This means you can extend your jump by landing as late as possible, ideally pressing enter on the same frame you will hit the ground. It’s easy enough to predict when that last possible frame is, so we only need to consider pressing enter on that one frame.
We’ve optimized the ramp, the flight and the landing, but there is one more aspect we need to look at: the lift-off. The way the lift-off works is that there is a specific optimal point along the ramp where the game expects you to press the down direction to jump, and depending on how close your jumping point is to that optimal point, you get awarded some number of “lift-off frames”, between 1 and 8, or 0 if you miss the jump entirely:
if !mem.ski_jump_lift_off_frames_calculated {
let deviation = clamp_value((mem.position_vec.z.raw() as i16 - 0x22f0).abs() / 0x60, 0, 7) as u8;
if !mem.ski_jump_never_lifted_off_flag {
mem.ski_jump_lift_off_frames = 8 - deviation;
}
mem.ski_jump_lift_off_frames_calculated = true;
}
During these lift-off frames, the game inverts gravity, pulling you up instead of down, and additionally doesn’t apply any vertical drag. This is hugely beneficial, so we want to always get all 8 possible lift-off frames. That means we only need to consider input sequences which achieve that, and can immediately discard any inputs which lift off at the wrong time.
All of these observations limit which inputs we need to consider at any given point, and drastically cut down on the number of possibilities. With this, and a whole lot more searching, we can finally get really good results:
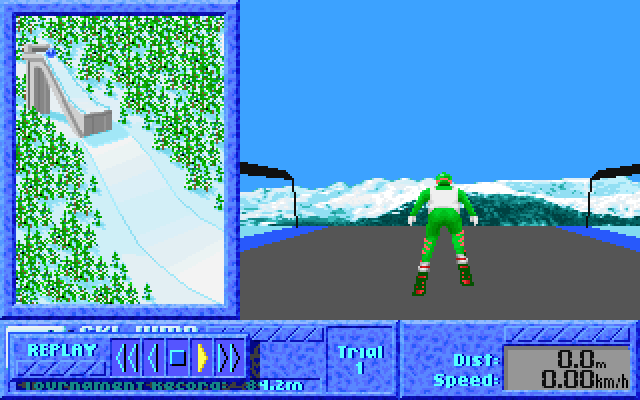
This attempt looks very optimized: It goes down the middle of the ramp, gains maximum lift-off, holds the ski angle perfectly parallel throughout the jump, and finally lands on the last possible frame. I’d wager this is farther than anyone has ever jumped in this game before, and is probably close to what is theoretically possible to achieve.
In order to go further, I considered throwing even more compute at the problem, likely with very heavy diminishing returns. The jump above took a couple of hours to find running on my home computer, with lots of jumps just 0.1m shorter than it. So instead of applying more brute force, I instead tried to apply more brain power, to find more unorthodox ways to optimize.
The wiggle technique
One aspect of the simulation that caught my eye was the way sideways motion is applied while sliding down the ramp. The corresponding logic looks like this:
mem.lr_random_deflection = clamp_value(mem.lr_random_deflection + if mem.state_frame_count % 2 == 0 { -1 } else { 1 } * (next_xor_rng_value(mem) % 0x18) as i16, -0x28, 0x28);
next_xor_rng_value(mem);
left_right_drift = Fixed16::from_raw_i16(-0x18 * inputs.x as i16 + mem.lr_random_deflection);
[...]
if mem.is_grounded {
let side_movement_vec = Vec3Fixed16::cross_product(mem.normalized_velocity_vec, mem.surface_normal_vec);
let left_right_drift_vec = side_movement_vec * left_right_drift;
accelecration_vec = accelecration_vec + left_right_drift_vec;
}
The game chooses a random deflection due to wind, and combines it with the player’s left/right input to determine the overall left/right drift for that frame. It then calculates a vector orthogonal to the current movement direction, scales it according to the desired drift, and adds it to the acceleration for this frame. The way this sideways movement is applied is typically called strafing, more commonly observed in first-person games.
Notably, because the sideways motion is essentially additional velocity you gain on top of the other forces applied to the jumper, sideways movement increases your overall speed. This effect is known as strafe-running, a classic technique in early first-person games to move faster by going diagonally, using both the forwards and the sideways velocity simultaneously.
In the context of this ski jumping simulation, we can exploit strafing in a similar way to build more speed: By moving sideways as much as we can, we generate additional speed which leads to a longer jump. However, since we can’t change the facing direction, that additional speed doesn’t seem to be too beneficial at first glance, since it points in a direction that doesn’t count towards the length of the jump. But this is only true on the first frame: Once we start moving diagonally along the ramp, if we start steering in the opposite direction, the sideways movement vector will also be diagonal, and parts of it will point forward, effectively increasing our speed down the ramp.
What we end up with is what I lovingly call the “wiggle technique”: By steering left and right quickly, we can build up additional speed through strafing, and then redirect that speed forwards, generating more velocity down the ramp and jumping farther.
To incorporate this technique into the search, I encouraged it to choose maximum left/right inputs on every frame down the ramp, and let it optimize for the maximum total velocity, even if that velocity doesn’t point in the right direction yet. Doing this, and running the search for a couple more hours, yielded a surprisingly underwhelming result: Only an improvement of 0.1m compared to the best previous attempt shown above. The reason for this is that through the brute-force search, it actually already used the wiggle technique on its own! When observing the replay above carefully, you can see how it oscillates left and right while going down the ramp, building speed through the wiggles.
So this record is actually already more optimal than I thought, but there’s one more ace up my sleeve.
Going farther by slowing down?
So far, my optimizations were focused on maximizing speed. This is for good reason, because in this simulation of what boils down to projectile motion, your distance is very directly a function of your speed, and there are not a lot of other confounding factors.
However, this analysis is only correct in an idealized continuous simulation, whereas the game’s simulation happens in discrete steps. Let’s look at the logic that handles the landing and determining the final distance:
let diaxcx = mem.position_vec - (cur_track_segment_vertices_relative[segment_square] + JMPTRACK_DATA[mem.jmptrack_cur_segment].position);
let di = -Vec3Fixed16::dot_product(mem.surface_normal_vec, diaxcx);
if di.raw() > 2 {
mem.is_grounded = true;
mem.position_vec = mem.position_vec + (mem.surface_normal_vec * di);
let si = Vec3Fixed16::dot_product_late_truncate(mem.surface_normal_vec, mem.raw_velocity_vec);
mem.raw_velocity_vec = mem.raw_velocity_vec - (mem.surface_normal_vec * si);
}
After updating the jumper’s position, the game performs this check to detect when the jumper is below the ground surface they are on top of, and then sets the grounded flag, as well as adjusting the position and velocity to snap the jumper up onto the surface. Whatever position the jumper ends up with after this process is the final distance that gets recorded.
Notably, that means the final distance is not actually the precise intersection point of the trajectory with the ground, but instead whatever the position of the jumper is after the frame when they hit the ground. This opens the door for a sneaky optimization: generally slowing down will still reduce the distance, but since drag also applies in the vertical direction, if we are able to slow down just enough to delay hitting the ground by one additional frame, we can accumulate one more frame’s worth of distance before the final measurement, potentially leading to a greater distance overall.
So what we want to do is still reduce drag as much as possible in the early parts of the jump to build distance, but then towards the end start deliberately incurring additional drag to slow the descent, just enough so that our final airborne frame ends just above the ground, and we get an additional frame of distance before landing.
Whether or not this actually improves the overall distance depends on how well the alignment already works out out-of-the-box. If the jump already happens to end close to the ground naturally, the potential for optimization is very small. Also, if we need to spend a lot of time increasing drag to stay in the air for that additional frame, the distance lost to lower speed might end up outweighing the distance gained by the additional frame.
For any given jump trajectory, whether, when, and how to brake is not at all obvious. To get an idea of what’s possible, I started by creating a heuristic, which given the initial position and velocity, estimates what the maximum possible landing distance will be. For that, it assumes it can achieve whichever drag value it wants at any frame, without worrying about whether the RNG actually allows it to occur, and tests out when it needs to start applying more drag to end up with the longest distance.
This heuristic is cheaper to run than doing an actual simulation, and gives some upper bound for the distance that can be achieved. I then ran a search using only that heuristic, simulating all attempts only up to when they lift off, and estimating the best possible result from there. Doing this gave me some upper bound on the possible distance, and also a list of favorable RNG seed values which can produce attempts that are fast enough down the ramp to allow those potentially far jumps.
By narrowing down the search to only those favorable values, it sped up the process of doing full simulations, and using the heuristic converted the search into an A* algorithm, discarding paths where good results are no longer achievable according to the heuristic. And I eventually struck gold:
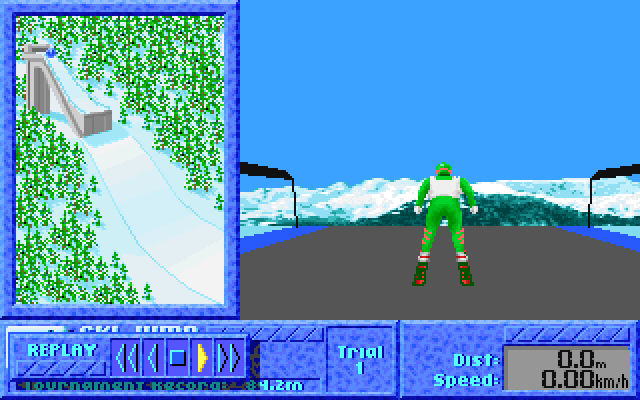
This distance of 113.8m matches the upper bounds the heuristics produced, so we can’t expect any farther jumps. One can clearly see that at the end of the flight, it changes the ski angle to create more drag, and also starts the landing animation exactly 9 frames before touching the ground, which is the maximum time allowed before crashing.
When doing a frame-by-frame comparison with the previous record, they are almost identical up to the jump. Due to the additional drag created before landing, the new record loses about 1m of distance, but it then gains an additional 1.3m of distance by being in the air for one more frame, overall coming out ahead.
The obvious next question is whether the same optimization is also possible during lift-off when leaving the ground. The idea is that by staying on the ramp for an additional frame, you could delay falling and therefore travel farther. However, it turns out that the alignment with the ramp is pretty much perfect already out-of-the-box, with the last frame on the ramp ending very close to the edge. So there is no more potential for optimization like this, and the result we have is as good as it’s going to get.
If you want to load up the replay in your own game, you can find it here.
Conclusion
Taking a step back, the gain over the jump I showed initially and performed in a couple minutes of trying is not actually that big, the incremental improvements trying to squeeze out the last bits of distance were even smaller, and the end result honestly doesn’t look that impressive. In the end, this was never about creating an impressive looking ski jump, but about learning how the game works. The process of taking it apart and deeply understanding its mechanics is what made this project enjoyable, and left me with a new appreciation for the creativity and ingenuity that went into creating it and making it work with the limited hardware available at the time.
It’s worth noting that the final resulting jump is not guaranteed to be optimal, and is just as far as I’m willing to push it to feel satisfied with the result. There may still be optimizations hidden that I didn’t think of, parts of the search space that were left unexplored, and I invite you to try and beat it if you want :)
Bonus: Glitches
Being a fairly vanilla physics simulation, there didn’t end up being a lot of oversights and unintended mechanics I found. The two that ended up being useful have already been described above, but I want to show off one additional glitch that sadly ended up not working out.
The idea behind it is based on how the track is represented in the game. Both the ramp and the ground are made up of segments, and each segment has 3 rectangular faces next to each other. Only the middle of these rectangles is the track the jumper uses, the rectangles to the left and right are the out-of-bounds areas, and touching them leads to an immediate crash. Those out-of-bounds rectangles are what causes the jumper to crash when going off the ramp (the fences left and right are visual-only), and it is also what causes the crash on the forest area to the left and the right of the landing zone.
However, these out-of-bounds areas only have a limited width, and don’t extend infinitely to either side. The game continues to draw the forest further to the side, but the collision surface ends eventually. The game has some precautions for this case, and can actually detect when the jumper is beyond the left or right edge of the geometry, but the code that handles these cases contains a bug:
load_next_geometry_segment(mem, mem.jmptrack_cur_segment);
mem.segment_square = calc_player_segment_square(mem, mem.position_vec);
if mem.segment_square == 0x82 { // off to the side, limit to inbounds
mem.segment_square = 2;
} else if mem.segment_square == 0x83 {
mem.segment_square = 0;
}
When it determines that the player is beyond the edge, it clamps the values to one of the three rectangles. However, it happens to choose the wrong one, using the left-side out-of-bounds surface when going off to the right and the right-side surface when going to the left. This means there is an improper collision check in these out-of-bounds areas, and if we steer sharply at the end of the ramp in order to jump as diagonal as possible, we can reach these areas. The hope is that by not colliding with the ground, we can keep falling and accumulating distance, eventually underflowing the fixed point values used to store the vertical position and coming back from the top at a much larger distance:
Unfortunately, this doesn’t lead to anything useful. The way the collision checks are implemented essentially assumes the active floor rectangle is a plane that extends infinitely in all directions. Due to the side rectangles being at a slight angle and the game choosing the opposite side’s floor rectangle, the jumper clips through the ground and only collides with the ground once the plane formed by the opposite side’s rectangle intersects. Since this is still an out-of-bounds rectangle though, landing on it is impossible and causes an immediate tumble with no hope of having the score count.